Câu hỏi 601931:
A. Không bác bỏ H0
B. Không chấp nhận H1
C. Chấp nhận H1
Lý thuyết xác suất và thống kê toán - EG11 (129)
Câu hỏi 601932:
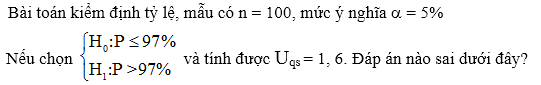
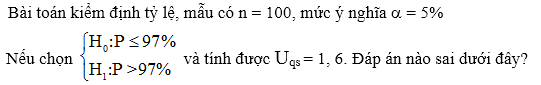
Giá trị nào dưới đây thích hợp với mức ý nghĩa trong kiểm định giả thuyết thống kê?
A. 0,5
B. 0,01
C. 0,95
D. 0,9
Câu hỏi 601933:
Đáp án nào đúng dưới đây?
Tìm hiểu 100 sinh viên đi làm thêm , thấy có 42 nữ với độ tin cậy 90%, tìm khoảng tin cậy đối xứng theo tỷ lệ (p) nữ trong số những người đi làm thêm?
A. 0,42 - 1,96 .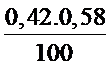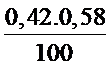 
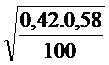≤ P ≤ 0,42 + 1,96 . 
≤ P ≤ 0,42 + 1,96 . B. 0,42 - 1,645 . 
≤ P ≤ 0,42 + 1,645 . 
≤ P ≤ 0,42 + 1,645 . C. 0,42 - 1,96 . 
≤ P ≤ 0,42 + 1,645 .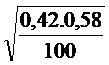 
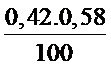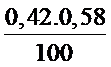
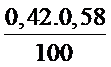≤ P ≤ 0,42 + 1,645 . D. 0,42 - 1,645 . 
≤ P ≤ 0,42 + 1,96 .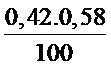 
≤ P ≤ 0,42 + 1,96 . Câu hỏi 601934:
Đối với bài toán ước lượng kỳ vọng của biến ngẫu nhiên có phân phối chuẩn chưa biết V(X) (mẫu có n <30) ). Đáp án nào đúng dưới đây?
A. T ~ T
B. 
C. Tất cả các đáp án đều đúng
Câu hỏi 601935:
Biến ngẫu nhiên X có phân phối Poisson P ( 
) với = 29
Khẳng định nào sau đây đúng?
A. P (19 < X < 39) ≥ 0,71
B. P (19 < X < 39) > 0,72
C. P (19 < X < 39) < 0,81
Câu hỏi 601936:
Biến ngẫu nhiên hai chiều rời rạc (X, Y) có bảng phân phối xác suất.
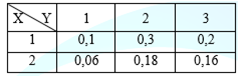
E(X) = ?
A. 2,2
B. 2,5
C. 2,4
D. 2,3
Câu hỏi 601937:
Biến ngẫu nhiên X có phân phối nhị thức B (n,p). n = 1000, p = 0,01. Đáp án nào đúng dưới đây?
A. P (0 < X < 20) > 0,90
B. P (0 < X < 20) ≥ 0,901
C. P (0 < X < 20) > 0,902
Câu hỏi 601938:
Cho biến ngẫu nhiên hai chiều rời rạc (X, Y) với các giả thiết
P (X = 2, Y = 4) = 0,2
P (X = 2, Y = 5) = 0,3
P(X=3,Y=4)=0,4
P(X = 3, Y = 5) = A
Khẳng định nào sau đây đúng?
A. A = 0,2
B. A = 0,15
C. A = 0,1
Câu hỏi 601939:
Biến ngẫu nhiên hai chiều rời rạc (X, Y) có bảng phân phối xác suất
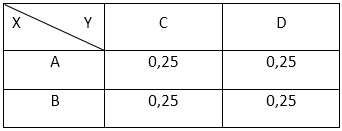
Đáp án nào sai dưới đây?
A. Biến ngẫu nhiên X, Y phụ thuộc
B. Cov (X, Y) = 0 với bất kỳ A # B; C # D
C. Biến ngẫu nhiên X, Y độc lập
Câu hỏi 601940:
Biến ngẫu nhiên hai chiều rời rạc (X, Y) có bảng phân phối xác suất
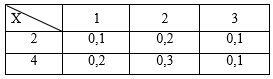
Khẳng định nào sau đây đúng?
A. E (X) = 3
B. P (X > 2) = 0,4
C. E (X) = 3,2
Câu hỏi 601941:
Biến ngẫu nhiên X liên tục có hàm phân phối xác suất
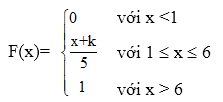
Khẳng định nào sau đây là đúng?
A. E (X) = 3
B. k = 1
C. k = -1
Câu hỏi 601942:
Biến ngẫu nhiên rời rạc X có bảng phân phối xác suất
|
X |
-2 |
0 |
4 |
|
Pi |
0,2 |
P2 |
P3 |
Với E (X) =1,6
Khẳng định nào là đúng?
A. P2 = 0,2 P3 = 0,6
B. P2 = 0,3 P3 = 0,5
C. P2 = 0,5 P3 = 0,3
Câu hỏi 601943:
Biến ngẫu nhiên liên tục X có hàm mật độ xác suất f(x) =
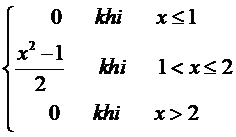
E(X) = ?
A. 1,1
B. 1,3
C. 1,2
D. 1,4
Câu hỏi 601944:
Biến ngẫu nhiên X liên tục có hàm mật độ xác suất f(x) không đổi bằng 0,1 trong khoảng ( -1, 9) còn ngoài khoảng đó thì bằng 0.
Khẳng định nào là sai?
A. E (X) = 5
B. E (X) = 4
C. 
Câu hỏi 601945:
Để biểu diễn quy luật phân phối của biến ngẫu nhiên người ta dùng:
A. Hàm mật độ xác suất
B. Bảng phân phối xác suất
C. Hàm phân phối xác suất
D. Cả 3 phương án trên
Câu hỏi 601946:
Một hộp có 4 bi đỏ và 6 bi vàng. Lấy ngẫu nhiên ra 2 viên bi. Quy luật phân phối xác suất của số bi vàng có thể lấy ra là :
A. 
B. 
C. 
D. 
Câu hỏi 601947:
Cho X ~ N (1, 1) ; Y = X – 2.
Khẳng định nào là đúng?
A. Y~ N (-1, -1)
B. E (XY) = -1
C. Y~ N (-1, 1)
D. E (XY) = 0.1
Câu hỏi 601948:
Biến ngẫu nhiên liên tục X có hàm mật độ xác suất
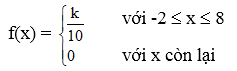
Khẳng định nào là sai?
A.
k = 1
k = 1
B. k = 2
C. E (X) = 3
Câu hỏi 601949:
Cho X ~ N (0, 2) ; Y ~ N (10, 2).
Khẳng định nào là sai?
A. (X + Y) ~ N (10; 4) nếu X, Y độc lập
B. E (XY) = 0
C. E (Y2 + X2) = 104
Câu hỏi 601950:
Biến ngẫu nhiên rời rạc X có bảng phân phối xác suất.
F(X) = ?
A. 
B. 
C. 
D. 
DONATE
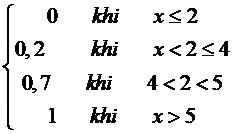
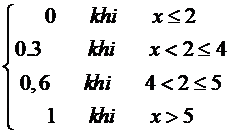
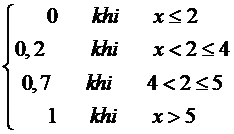
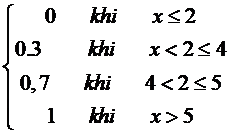
Để giúp chúng tôi phát triển sản phẩm tốt hơn, đạt kết quả học tập cao hơn
Bản tin HOU-TV số 06 năm 2025
