Câu hỏi 730016:
Cho mô hình thu nhập quốc dân của 2 thành phần:
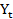 =
= 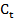 +
+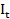 ,
, 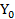 = 2500
= 2500
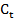 = 0,8
= 0,8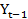 +400
+400
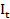 = 0,1
= 0,1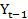 +300
+300
Tìm mức ổn định cân bằng Y= C+I của mô hình trên.
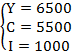
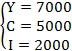
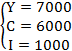
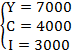
Cho mô hình thu nhập quốc dân của 2 thành phần:
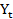 =
= 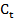 +
+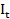 ,
, 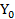 = 2500
= 2500
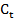 = 0,8
= 0,8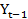 +400
+400
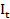 = 0,1
= 0,1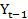 +300
+300
Tìm mức ổn định cân bằng Y= C+I của mô hình trên.
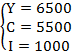
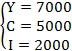
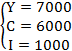
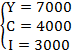
Tính diện tích S của hình phẳng bị giới hạn bởi các đường y=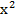 , y=
, y=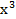 .
.
Giải phương trình
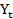 = 5
= 5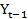 +12 với
+12 với 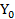 =18.
=18.
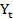 = 22(
= 22(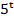 )-4
)-4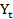 = 21(
= 21(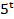 )-3
)-3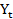 = 20(
= 20(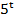 )-2
)-2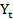 = 15(
= 15(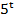 )+3
)+3Mức thu nhập quốc dân 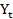 của 1 quốc gia tại năm t được xác định bởi
của 1 quốc gia tại năm t được xác định bởi
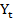 =
= 
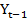 +150.
+150.
Biết mức thu nhập tại năm đầu tiên vào khoảng 100 tỷ USD, hãy xác định mức thu nhập quốc dân của quốc gia này 60 năm sau kể từ năm đầu tiên.
Cho mô hinh thu nhập quốc dân:
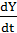 = 0,5(C+I-Y)
= 0,5(C+I-Y)
C= 0,7Y + 500
I= 0,2Y + 500
Biết mức thu nhập ban đầu Y(0)= 2000, tính mức chi tiêu C tại t=10.
Cho ma trận
A= 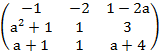 .
.
Tìm a để định thức det(A) của ma trận A đạt giá trị nhỏ nhất.
Cho hàm chi phí trung bình AC= 3Q+5+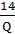 . Tìm chi phí cận biên MC tại Q=5.
. Tìm chi phí cận biên MC tại Q=5.
Cho các phương trình cung, cầu 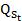 =0,4
=0,4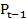 -12
-12
, 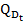 = -0,8
= -0,8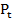 +60. Biết thị trường luôn ở trạng thái cân bằng tại mọi thời điểm t và giá khởi điểm
+60. Biết thị trường luôn ở trạng thái cân bằng tại mọi thời điểm t và giá khởi điểm
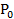 =85, hãy xác định lượng cân bằng cung cầu
=85, hãy xác định lượng cân bằng cung cầu
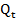 tại năm t=11.
tại năm t=11.
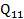 = 12,0097
= 12,0097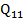 = 12,0098
= 12,0098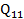 = 12,009
= 12,009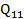 = 12,0096
= 12,0096Cho phương trình
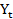 = -
= -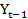 +8 với
+8 với 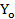 =20. Tìm
=20. Tìm 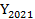 .
.
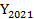 = 20
= 20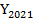 = 12
= 12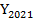 = -12
= -12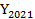 = 18
= 18Cho mô hình thu nhập quốc dân tại năm t:
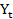 =
= 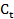 +
+ 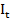
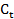 = 0,7
= 0,7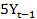 +550
+550
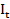 = 250
= 250
Biết mức thu nhập khởi điểm 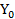 =480, tính sự thay đổi của mức thu nhập từ năm t=5 đến năm t=11.
=480, tính sự thay đổi của mức thu nhập từ năm t=5 đến năm t=11.
Cho các phương trình cung cầu 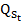 =
=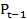 - 38
- 38
, 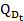 = -2
= -2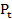 +142. Biết thị trường luôn ở trạng thái cân bằng tại mọi thời điểm và giá khởi điểm năm đầu tiên
+142. Biết thị trường luôn ở trạng thái cân bằng tại mọi thời điểm và giá khởi điểm năm đầu tiên 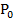 =55. Hỏi lượng cân bằng cung cầu tại năm t=10 thay đổi thế nào so với lượng cân bằng cung cầu năm đầu tiên?
=55. Hỏi lượng cân bằng cung cầu tại năm t=10 thay đổi thế nào so với lượng cân bằng cung cầu năm đầu tiên?
Tìm max/min{8x+10y},
v.đ.k
2x+y≤8
x+2y≤7
4x+5y≥10
x≥0
0≤y≤3
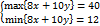
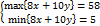
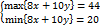
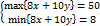
Tìm max/min{6x+2y}, v.đ.k
x-y≥0
3x+y≥8
x+y≤8
x≥0
y≥0
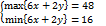
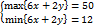
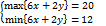
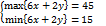
Tính diện tích S của hình phẳng bị giới hạn bởi các đường y=0, y=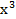 +
+ , x=1, x=3.
, x=1, x=3.
Tính tích phân
I= 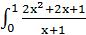 dx
dx
Tính diện tích S của hình phẳng bị giới hạn bởi các đường y= 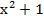 , x+y=3.
, x+y=3.
Biết hàm chi phí cận biên của 1 công ty là:
MC= 3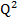 - 2Q + 5, trong đó Q là lượng sản phẩm đầu ra, và chi phí cố định FC= 100. Tìm hàm tổng chi phí TC.
- 2Q + 5, trong đó Q là lượng sản phẩm đầu ra, và chi phí cố định FC= 100. Tìm hàm tổng chi phí TC.
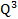 -
-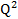 + 5Q + 100
+ 5Q + 100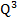 -
- 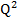 + 5Q + 100
+ 5Q + 100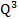 +
+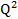 + 5Q + 100
+ 5Q + 100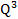 +
+ 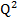 - 5Q - 100
- 5Q - 100Cho A =  . Tìm
. Tìm 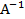 .
.
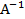 =
= 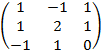
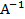 =
= 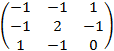
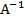 =
= 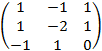
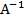 =
= 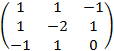
Cho các ma trận
A= 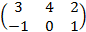 ,
,
B= 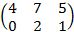 . Tìm ma trận X làm thỏa mãn phương trình
. Tìm ma trận X làm thỏa mãn phương trình
2A + 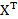 = 3B
= 3B




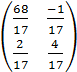
Tìm ma trận X làm thỏa mãn hệ thức:
3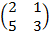 X=2X+
X=2X+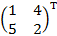
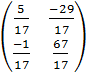
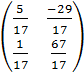
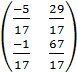
Để giúp chúng tôi phát triển sản phẩm tốt hơn, đạt kết quả học tập cao hơn















