Câu hỏi 573094:
Tính I = 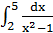 .
.
Tính I = 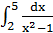 .
.
Tính tích phân
I= 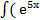 +
+ 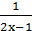 )dx
)dx
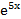 +
+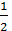 ln|2x-1| + C
ln|2x-1| + C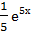 +
+
 ln|2x-1| + C
ln|2x-1| + C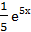 +
+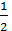 ln|2x-1|
ln|2x-1|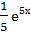 +
+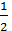 ln|2x-1| + C
ln|2x-1| + CCho biết khuynh hướng tiêu dùng biên
MPC= 0,6 + 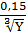 và mức tiêu dùng C= 95 khi thu nhập Y= 125. Tìm hàm tiêu dùng C.
và mức tiêu dùng C= 95 khi thu nhập Y= 125. Tìm hàm tiêu dùng C.
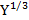
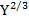
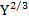
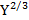
Cho hàm sản xuất
Q= 10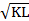 + 7L, với vốn K=90 và lượng nhân công L= 40. Từ ý nghĩa của đạo hàm riêng, hãy ước lượng sự thay đổi của sản lượng Q khi K tăng lên 3 đơn vị, còn L giảm đi 2 đơn vị.
+ 7L, với vốn K=90 và lượng nhân công L= 40. Từ ý nghĩa của đạo hàm riêng, hãy ước lượng sự thay đổi của sản lượng Q khi K tăng lên 3 đơn vị, còn L giảm đi 2 đơn vị.
Cho hàm
z= 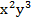 – 10xy +
– 10xy + 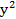 . Tính
. Tính 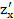 và
và 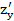 tại điểm (2,3).
tại điểm (2,3).
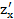 (2,3)= 108;
(2,3)= 108;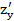 (2,3)= 104
(2,3)= 104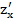 (2,3)= 74;
(2,3)= 74;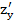 (2,3)= 93
(2,3)= 93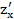 (2,3)= 70;
(2,3)= 70;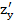 (2,3)= 92
(2,3)= 92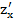 (2,3)= 78;
(2,3)= 78;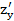 (2,3)= 94
(2,3)= 94Cho hàm sản xuất
Q= 600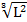 -5L, trong đó Q là sản lượng (số lượng đơn vị sản phẩm của 1 loại hàng hóa), L là số nhân công. Tính sản lượng lao động biên
-5L, trong đó Q là sản lượng (số lượng đơn vị sản phẩm của 1 loại hàng hóa), L là số nhân công. Tính sản lượng lao động biên
MPL tại L= 125.
Cho hàm cầu
P= -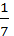 Q + 3. Tính giá P, biết lượng cầu Q=10.
Q + 3. Tính giá P, biết lượng cầu Q=10.
Một mô hình kinh tế vĩ mô được cho bởi hệ phương trình tuyến tính Ax=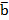 , với các ma trận
, với các ma trận
A= 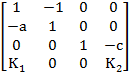 ,
,
x= 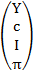 ,
, 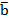 =
= 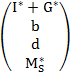 .
.
Hãy xác định lãi suất 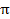 của nhu cầu đầu tư
của nhu cầu đầu tư
I= c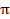 + d, ở đây 0<a<1,
+ d, ở đây 0<a<1,
b>0, c<0, d>0, 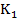 >0,
>0, 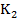 <0,
<0, 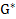 >0,
>0, 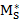 >0.
>0.
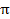 =
=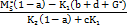
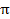 =
=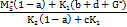
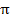 =
=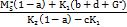
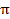 =
=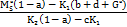
Với giá trị nào của m, hệ phương trình:
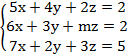
không có nghiệm duy nhất?
Cho các ma trận
A= 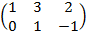
B= 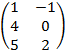
Tính 2A+3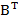 .
.
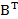 =
=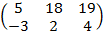
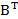 =
=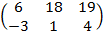
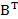 =
=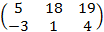
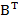 =
=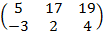
Cho ma trận A có nghịch đảo 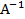 , tìm ma trận X thỏa mãn hệ thức AX-2B=C, với
, tìm ma trận X thỏa mãn hệ thức AX-2B=C, với
A= 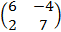 ,
,
B= 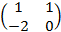 ,
,
C= 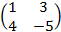 .
.
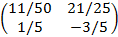
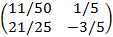
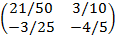
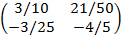
Cho A= (1 2 4),
B= (5 6 7). Tính 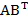 .
.
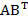 = (48)
= (48)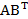 = 48
= 48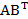 = (45)
= (45)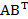 = 45
= 45Cho ma trận
A= 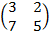 và hàm số f(x)=
và hàm số f(x)= 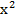 -8x+1.
-8x+1.
Tính f(A).
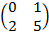

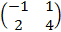
Cho thị trường hàng hóa C= 0,8Y + 60,
I= -30π + 740 và thị trường tiền tệ 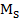 =4000,
=4000,
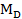 = 0,15Y-20π+3825.
= 0,15Y-20π+3825.
Xác định thu nhập quốc dân Y và lãi suất π với giả thiết thị trường hàng hóa và thị trường tiền tệ đều ở trạng thái cân bằng.
Cho ma trận A= 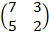
Tìm ma trận nghịch đảo
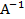 .
.
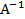 =
= 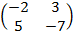
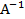 =
= 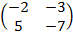
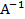 =
= 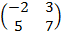
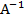 =
= 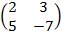
Tìm a để hệ phương trình :
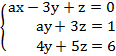
có nghiệm duy nhất.
Cho A= 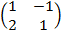
B= 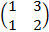
Tính E= AB - BA.
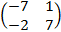
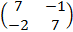
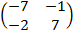
Tìm tập xác định E của hàm
z= 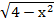 – ln(1-
– ln(1-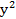 )
)
Cho hàm
z= ln(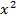 +
+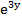 -16).
-16).
Tính z(4, 2).
Một hãng sản xuất 2 loại sản phẩm 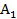 ,
, 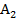 với các hàm cầu là
với các hàm cầu là 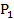 = 300-2
= 300-2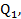
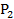 = 200-
= 200-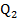 , và hàm tổng chi phí là
, và hàm tổng chi phí là
TC= 5000+100Q với Q= 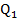 +
+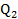 . Ở đây
. Ở đây 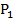 ,
,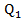 ,
,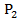 ,
,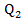 là giá và lượng sản phẩm đối với các sản phẩm
là giá và lượng sản phẩm đối với các sản phẩm 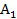 ,
,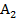 tương ứng. Tìm
tương ứng. Tìm 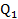 ,
,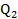 để hãng đạt được lợi nhuận cực đại.
để hãng đạt được lợi nhuận cực đại.
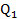 =40,
=40,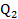 =60
=60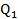 =30,
=30,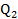 =70
=70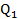 =60,
=60,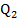 =40
=40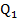 =
= 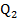 = 50
= 50Để giúp chúng tôi phát triển sản phẩm tốt hơn, đạt kết quả học tập cao hơn















