Câu hỏi 573128:
Biết mức thu nhập Y là tổng hòa của 2 mức chi tiêu C và tiết kiệm S và C= 0,05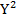 + 0,2
+ 0,2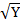 + 60.
+ 60.
Tính khuynh hướng tiêu dùng biên MPC và khuynh hướng tiết kiệm biên MPS tại Y= 25.
MPS = 1,48
MPS = -1,5
MPS = -1,54
MPS = -1,52
Biết mức thu nhập Y là tổng hòa của 2 mức chi tiêu C và tiết kiệm S và C= 0,05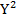 + 0,2
+ 0,2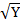 + 60.
+ 60.
Tính khuynh hướng tiêu dùng biên MPC và khuynh hướng tiết kiệm biên MPS tại Y= 25.
Cho hàm cầu
P= -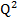 -6Q+154. Tìm độ co giãn E của cầu theo giá, khi giá P=63.
-6Q+154. Tìm độ co giãn E của cầu theo giá, khi giá P=63.
Cho hàm chi phí trung bình
AC= 2Q + 8 + 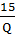 . Từ ý nghĩa của chi phí cận biên, hãy ước lượng sự thay đổi của tổng chi phí TC khi lượng hàng giảm đi 3 đơn vị từ lượng ban đầu Q0=15.
. Từ ý nghĩa của chi phí cận biên, hãy ước lượng sự thay đổi của tổng chi phí TC khi lượng hàng giảm đi 3 đơn vị từ lượng ban đầu Q0=15.
Hàm cầu và hàm tổng chi phí TC được cho bởi công thức:
4P + Q – 16 = 0 và
TC= 4 + 2Q -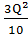 +
+ 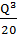 .
.
Tính tổng doanh thu cận biên MR và chi phí cận biên MC tại lượng hàng Q làm cực đại lợi nhuận.
Một mô hình kinh tế vĩ mô được cho bởi hệ phương trình tuyến tính Ax=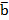 , với các ma trận
, với các ma trận
A= 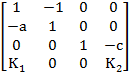 ,
,
x= 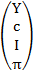 ,
, 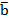 =
= 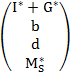 .
.
Hãy xác định lãi suất 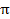 của nhu cầu đầu tư
của nhu cầu đầu tư
I= c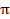 + d, ở đây 0<a<1,
+ d, ở đây 0<a<1,
b>0, c<0, d>0, 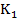 >0,
>0, 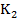 <0,
<0, 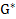 >0,
>0, 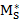 >0.
>0.
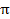 =
=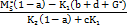
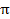 =
=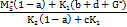
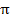 =
=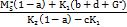
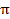 =
=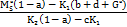
Cho hàm cầu thỏa mãn phương trình 2Q+P=35 và hàm chi phí trung bình
AC= + 7. Tìm hàm lợi nhuận
Sau cuộc đấu giá một người mua được chiếc bình cổ với giá 1575 triệu VND. Tính tỷ lệ phần trăm gia tăng của một chiếc bình, biết giá khởi điểm của nó khi đấu giá là 500 triệu VND.
Một chiếc xe hơi có giá trị xuất xưởng 1250 triệu VND, sau 2 năm nó được bán lại với giá 572 triệu VND. Hỏi chiếc xe bị giảm giá trị bao nhiêu phần trăm so với giá khởi điểm?
Giá của một mặt hàng trong năm tăng 8%, nhưng bị giảm 30% trong đợt xả hàng. Tổng thể mặt hàng này bị giảm bao nhiêu phần trăm giá trị?
Giá cổ phiếu trên thị trường chứng khoán của một công ty tăng 32% ở nửa đầu năm, nhưng giảm 18% ở nửa cuối năm. Biết giá cổ phiếu này trong phiên giao dịch cuối cùng ở cuối năm là 45.000 VND. Xác định giá trị của cổ phiếu tại phiên giao dịch đầu tiên ở thời điểm đầu năm.
Cho hàm cầu
P= 120 - 5Q. Tìm doanh thu cận biên MR tại Q=10.
Một nhà máy có chi phí cố định 300 USD mỗi tuần và chi phí biến đổi trên một đơn vị hàng VC= 3Q-42. Tìm lượng hàng Q sao cho chi phí trung bình mỗi tuần của nhà máy bị chịu ở mức thấp nhất.
Xét một nền kinh tế khép kín không có sự can thiệp của chính phủ, với hàm tiêu dùng C= 0,8Y + 50 và lượng đầu tư cố định theo kế hoạch I= 200. Tính mức thu nhập quốc dân Y.
Với một nền kinh tế khép kín không có sự can thiệp của chính phủ, với hàm tiêu dùng C= 0,5Y + 70 và lượng đầu tư cố định theo kế hoạch I= 450. Tính lượng tiết kiệm thu được S.
Với một nền kinh tế khép kín không có sự can thiệp của chính phủ, với hàm tiêu dùng C= 0,7Y + 40 và lượng đầu tư theo kế hoạch cố định I= 300. Tính lượng tiêu dùng.
Tính giá trị hiện tại So của 1 dòng thu nhập liên tục ở mức không đổi 2500 USD một năm, nếu tỷ lệ chiết khấu là 5% và tiền được chi trả trong 5 năm.
Cho các hàm cung, cầu
P= 2+ 15 và
P= -3+70. Tìm giá và lượng cân bằng.
Tổng sản phẩm thu nhập quốc dân năm (GNP) của 1 nước là 75.250 triệu USD được dự báo tăng 4,7% năm. Tổng dân số nước này là 152 triệu dân, dự báo tăng 2% năm. Hỏi sau ít nhất bao nhiêu năm, GNP trên đầu người nước này sẽ vượt 750 triệu USD?
Một công ty sản xuất 2 loại sản phẩm A, B từ 4 loại đơn vị nguyên liệu I, II, III, IV. Để sản xuất 1 đơn vị sản phẩm A cần 8 đơn vị nguyên liệu I, 5 đơn vị nguyên liệu II và 1 đơn vị nguyên liệu IV. Để sản xuất 1 đơn vị sản phẩm B cần 3 đơn vị nguyên liệu I, 4 đơn vị nguyên liệu II và 1 đơn vị nguyên liệu III. Tiền lãi thu được khi bán 1 đơn vị sản phẩm A là 5 triệu VND, khi bán 1 đơn vị sản phẩm B là 2 triệu VND. Hãy xây dựng phương án sản xuất tối ưu sao cho tổng số tiền lãi thu được là lớn nhất, biết dữ trữ các đơn vị nguyên liệu của công ty từ I đến IV lần lượt là 24; 20; 3 và 2,5 đơn vị.
Để giúp chúng tôi phát triển sản phẩm tốt hơn, đạt kết quả học tập cao hơn















